“曹冲称象”在中国几乎是妇孺皆知的故事。年仅六岁的曹冲,利用漂浮在水面上的物体的重力等于水对物体的浮力这一物理原理,解决了一个连许多有学问的成年人都一筹莫展的大难题,这不能不说是一个奇迹。可是,在那个年代(公元200年),虽然阿基米德原理已经发现了500年,但这一原理直到1627年才传入中国,小曹冲不可能知道这个原理,更不用说浮沉条件了。
实际上,聪明的曹冲所用的方法是“等量替换法”。用许多石头代替大象,在船舷上刻划记号,让大象与石头产生等量的效果,再一次一次称出石头的重量,使“大”转化为“小”,分而治之,这一难题就得到圆满的解决。
等量替换法是一种常用到的科学思维方法。这里再讲一个爱迪生的小故事。美国大发明家爱迪生有一位数学基础相当好的助手叫阿普顿。有一次,爱迪生把一只电灯泡的玻璃壳交给阿普顿,要他计算一下灯泡的容积。阿普顿看着梨形的灯泡壳,思索了好久之后,画出了灯泡壳的剖视图、立体图,画出了一条条复杂的曲线,测量了一个个数据,列出了一道道算式。经过几个小时的紧张计算,还未得出结果。爱迪生看后很不满意。只见爱迪生在灯泡壳里装满水,再把水倒进量杯,不到一分钟,就把灯泡的容积“算”出来了。这里,爱迪生用倒入量杯里的水的体积代替了灯泡壳的容积,用的也是等量替换法。
在实验室里,也常用等量替换法解决一些难题。比如,有一架不准的天平和几盒准确的砝码,怎样才能准确地称量一个物体的质量?可以这样做:先在天平左盘上放上侍测物体,在右盘上放上砝码,调节天平平衡。然后再从另一盒砝码中取出适量的砝码代替左盘中的待测物体,使天平再次平衡(右盘中的砝码不添也不减),则放在左盘砝码的质量就等于待测物体的质量。这里,在同样能使天平平衡的条件下,待测物体和左盘中的砝码进行了“等量替换”。
实际上,在课堂和日常生活中,同学们已经有意识或无意识地用过等量替换法。如,用量筒测量不规则物体的体积,用绳子拴上石块来测井的深度等,都是运用了这种方法。
等量替换的思维方法还可以帮助同学们巧妙地解题。下面来看一道题。
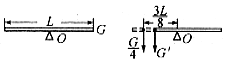
例 如图所示,一均匀直棒长为L,重为G,以其中点为支点,则棒处于平衡状态。现将其左端锯掉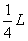 ,然后在左端挂一砝码,直棒仍处于平衡状态,则砝码重为( )
,然后在左端挂一砝码,直棒仍处于平衡状态,则砝码重为( )
A.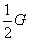 B.
B.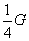 C.
C.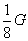 D.
D.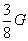
分析:设左端悬挂的砝码重为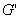 ,则重为
,则重为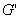 的砝码和锯掉的
的砝码和锯掉的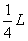 直棒对支点O的作用效果相同。因此在杠杆平衡的条件下有
直棒对支点O的作用效果相同。因此在杠杆平衡的条件下有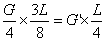 ,解得
,解得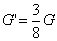
答案:D
以上的解法抓住了砝码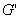 和锯掉的
和锯掉的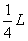 直棒对杠杆平衡的效果相同,利用等量替换的思想解决了问题。可见,掌握一种方法比多做几道题重要得多。
直棒对杠杆平衡的效果相同,利用等量替换的思想解决了问题。可见,掌握一种方法比多做几道题重要得多。
